A Bag Contains 5 Red Marbles 3 Green Marbles 2 Purple Marbles 2 Orange Marbles And 1 Blue Marble

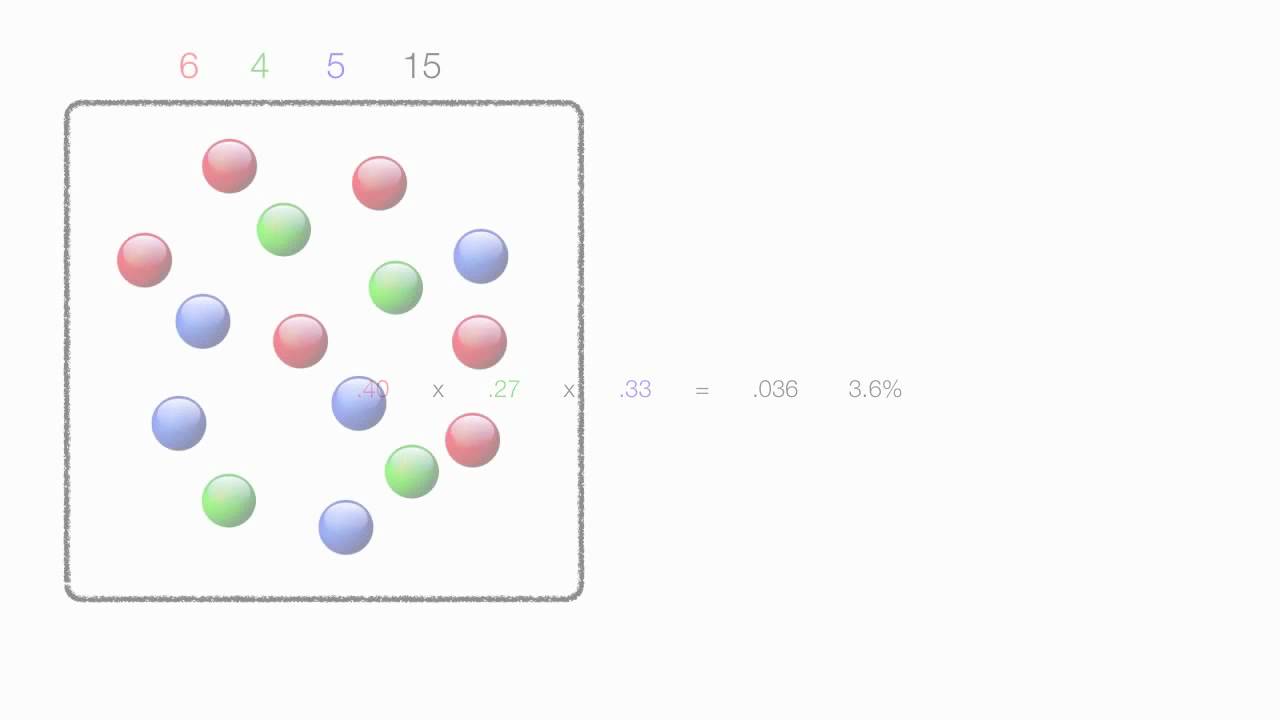
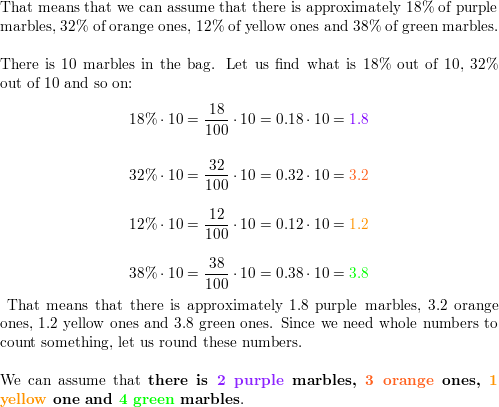Two consecutive draws are made from the bag without replacement of the first draw.

A bag contains 5 red marbles 3 green marbles 2 purple marbles 2 orange marbles and 1 blue marble.

Algebra linear inequalities and absolute value theoretical and experimental probability. Draws are made without replacement. A bag contains 3 red marbles 2 blue marbles and 5 green marbles. Also x 3 marbles have a scratch on them.

Two marbles are drawn without replacement from a jar containing 4 black and 6 white marbles. In this bag with x 2 5 marbles total x 1 are red. A bag contains 5 green marbles 8 red marbles 11 orange marbles 7 brown marbles and 12 blue marbles. Is it 8 27.

What is the probability of randomly selecting a blue marble then without replacing it randomly selecting a green marble. Find the probability that both are blue under each condition. Bag a contains 9 red marbles and 3 green marbles. 3 yellow marbles and 2 black marbles.

A jar contains 4 black marbles and 3 red marbles. A box contains 5 purple marbles 3 green marbles and 2 orange marbles. Two marbles are drawn without replacement. A bag contains 5 red marbles and 4 pink marbles.

First since we are dealing with the color orange and the rest according to the question we can say that we have only two sets of marbles. A bag contains 8 red marbles 5 blue marbles 8 yellow marbles and 6 green marbles. This is simple so first we set this problem up 2 red 3 blue 7 green 12 total marbles the formula for calculator probability is of favorable outcomes of possible outcomes the number of favorable outcomes we have is 3 because we are try. The probability of drawing a red marble from the original bag is equal to that.

A box contains 5 purple marbles 3 green marbles and 2 orange marbles. Report answers to 3 decimal places. A marble is randomly drawn and then replaced. A bag contains 5 blue marbles 4 red marbles and 3 orange marbles.

The first set is the orange and that contains just 3 orange marbles. What is the probability of choosing a red marble if a single choice is made from the bag. Draws are made without replacement. B find probabilities for p bb p br p rb p ww p at least one red p exactly one red 3.

The second set contains 5 blue and 4 red marbles making a total of 9. Two marbles are drawn one at a time from the bag. P 1st orange then green. A draw the tree diagram for the experiment.

A bag contains 3 red marbles 5 green marbles and 2 blue marbles. 5 red marbles 6 blue marbles 3 green marbles 4 black marbles 2 yellow marbles a marble will be drawn from the bag and replaced 100 times.